5.2 ANOVA
ANOVA-analyser kan ses på som en forenklet lineær regresjonsanalyse, der en undersøker om gjennomsnittsverdien til en kontinuerlig variabel er forskjellig i to eller flere grupper gitt ved en kategorisk grupperingsvariabel. Ett mulig eksempel er å teste om gjennomsnittslønnen er forskjellig for personer med hhv. lav, middels og høy utdannelse (benytter en variabel der utdanningsnivå deles inn i tre grupper).
Syntax:
anova <variabel> <variabelliste> [if <betingelse>] [,<opsjoner>]
Eksempel:
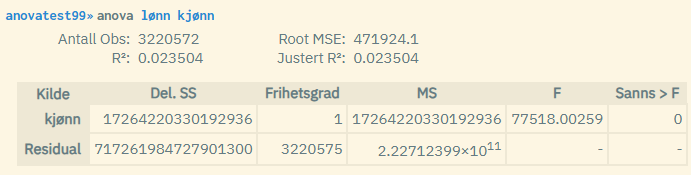
Eksempelet over viser en enkel analyse med kun én grupperingsvariabel, altså en enveis ANOVA-analyse. Denne viser at det er en signifikant forskjell i lønn mellom kategoriene til "kjønn", altså mellom menn og kvinner. Dette ser man av at p-verdien til F-testen er lik 0 (altså under 0.05). Man kan også teste den kontinuerlige variabelen opp mot to andre kategoriske variabler. Dette kalles toveis ANOVA-analyse.
Gjennom å bruke opsjonen posthoc, kan du kjøre en post hoc-analyse og i tillegg gjøre parvise sammenlikninger av snittet av den kategoriske variabelen målt over alle de respektive kategoriene for grupperingsvariabelen. Dette betyr at hver enkelt kategori blir sammenliknet direkte med alle de andre kategoriene:
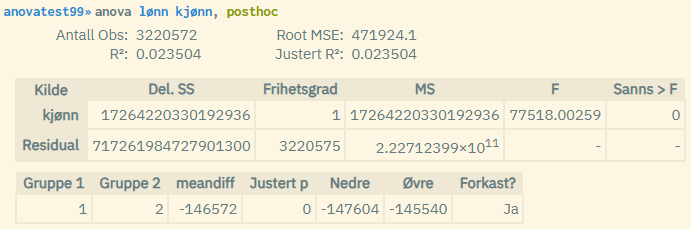
Post hoc-analysen viser i tillegg hva differansen i gjennomsnittet av lønn er mellom de to kategoriene mann og kvinne gitt ved verdiene 1 og 2. I tillegg vises det en justert p-verdi som viser om differansen er signifikant (p-verdi under 0.05). Dersom det står "Ja" i kolonnen "Forkast?", betyr dette at man forkaster nullhypostesen om ingen forskjell. Også et konfidensintervall vises for hver sammenlikning.
Post hoc kan også brukes på toveis ANOVA-analyse (da utvides listen med parvise sammenlikninger til å inkludere den ekstra variabelen):
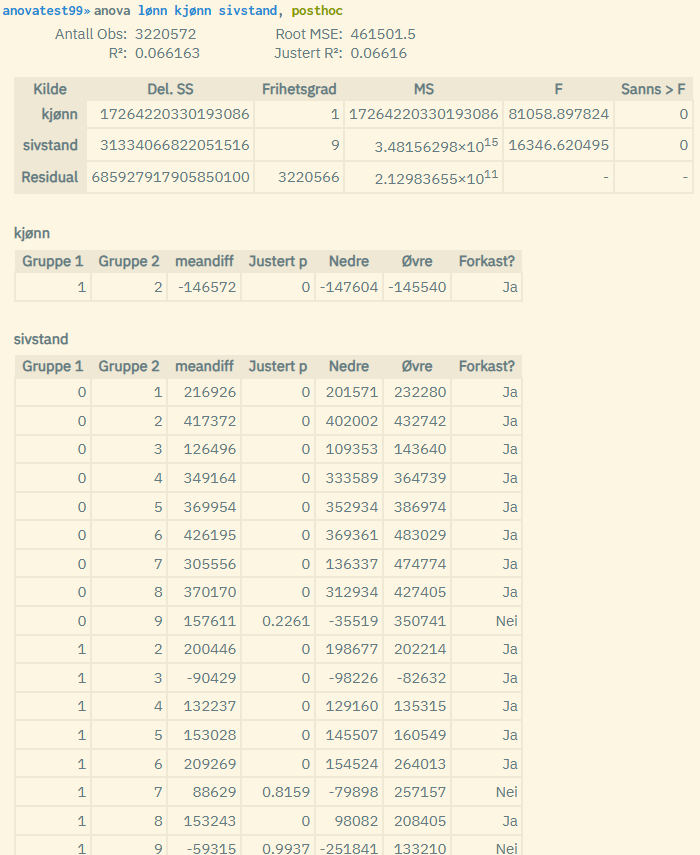
I den utvidede toveis ANOVA-analysen med post hoc, sjekker man både variablene kjønn og sivilstand. Variabelen sivilstand har 10 kategorier, og listen med parvise sammenlikninger blir da mye lengre (hele tabellen får ikke plass i denne eksempelvisningen). Som man kan se, er det signifikante forskjeller mellom de fleste sivilstand-kategoriene, men ikke alle. F.eks. er det ikke noen signifikant forskjell mellom sivilstand-kategoriene 0 og 9, 1 og 7, eller 1 og 9.
I kapittel 5.4 kan du lese mer om lineære regresjonsanalyser. Disse tar steget videre og estimerer effekten av hver kategori på en kontinuerlig variabel (responsvariabel) i forhold til en basis-/referansekategori for en gitt kategorisk variabel (forklaringsvariabel), der man kontrollerer for et sett med andre variabler som også har en effekt. Man sier altså noe om det er en positiv, negativ eller ingen effekt (i forhold til en referansekategori), i stedet for å bare sammenlikne gjennomsnitt. Lineære regresjonsanalyser kan også brukes til å se på effekten på en kontinuerlig variabel (responsvariabel) av en enhets økning i en eller flere kontinuerlige variabler (forklaringsvariabler).
Kilde:
Algoritmene for kommandoen anova baserer seg på funksjonen anova_lm som tar resultatet fra en OLS-estimering på de samme variablene som input. Opsjonen posthoc benytter en TukeyHSD-tilnærming som baserer seg på funksjonen pairwise_tukeyhsd. Begge funksjonene finner man i Statsmodels-modulen i Python.